New Approaches For Drug Substance Freezing And Storage
By Jeff Johnson, president, Biotech Design LLC
The significant growth of the biologic drug market, bolstered by the COVID-19 pandemic and the development of relevant vaccines, has led to a need for improved bulk drug substance (DS) freezing and frozen storage methods.
Freezing DS in conventional ultra-low temperature (ULT) freezers results in many inconsistencies within a single run — for example, some bottles freeze relatively fast while others are quite slow — which can lead to product quality concerns. In addition, freezing materials from ambient temperatures requires the removal of a large amount of heat, which taxes the refrigeration system. Conventional ULT storage freezers are not designed to handle this process. Such high strain can lead to frequent maintenance and/or greatly reduce service life.
After the DS has gone through the freezing process, it must be stored in long-term freezers. There are a number of storage freezer options available. An economic evaluation of the different options can lead to the optimum technology choice for each end user’s application.
First, let’s explore the latest technology for freezing DS from ambient temperatures. Then, we’ll look at equipment for storing already-frozen DS.
Part 1: Comparing Freezer Designs For Freezing Drug Substance
Standard ULT freezers that achieve a temperature of minus 80°C are designed to store already-frozen material with little additional capacity. When used for freezing DS from ambient temperatures, their freezing rates vary significantly with product load (from a few hours to several days) and from batch to batch depending on DS loading. Given the lack of capacity to remove heat effectively, long run times (48 to 72 hours) during a freezing cycle can result in permanent damage to the refrigeration system. Bottles also freeze at different rates, resulting in variability in DS quality.
To better understand the heat load and a freezer’s ability to handle it, the actual heat load for a freezer can be calculated. The first calculation is how much heat is transferred through a freezer’s walls with the chamber at minus 80°C and the outside ambient air at 25°C.
The base cabinet heat load (Q') is calculated using the following equation:
kf x As x ΔT/t = Q'
Where:
kf is the thermal conductivity.
As is the area.
ΔT is the change in temperature.
t is the wall thickness.
Plugging in the values of a standard ULT freezer cabinet results in the following equation:
0.020 W / (m - K) x 6.3 m2 x 105°C (105 K) / 0.127 m = 104 W
The same calculation can be repeated for the freezer door, yielding 30 W. Furthermore, there is additional heat loss across the door gasket of ~24 W, giving a total heat transferred into the cabinet from the outside of 158 watts:
Base cabinet wall (top, back, sides, and bottom) (104 W) + across the face of the door (30 W) + across the door gasket (24 W) = 158 W
A conventional ULT freezer’s refrigeration system is typically oversized to remove the cabinet heat load by 30% to 40%. This equates to a design load between 210 W and 243 W, leaving 52 W to 85 W as the freezer’s capacity or buffer for loading and freezing of warm product and/or temperature recoveries from door openings.
Another approach to freezing DS is to use a freezer designed specifically for the freezing process, such as a blast or controlled rate freezer. These freezers are designed to remove heat from large volumes of materials using forced air convection and are available from a number of suppliers, such as Cryometrix, FARRAR, Meissner, and Thermo Fisher Scientific. Blast freezers typically are designed to freeze at one freeze rate, while controlled rate freezers can be programmed to freeze and/or thaw according to a defined temperature profile. To calculate the capacity of this type of freezer, Figure 1 shows heat transfer loads (Q) for the cabinet, blower, door, and door jamb using the FARRAR Model 4000 Controlled Rate Chamber as an example.
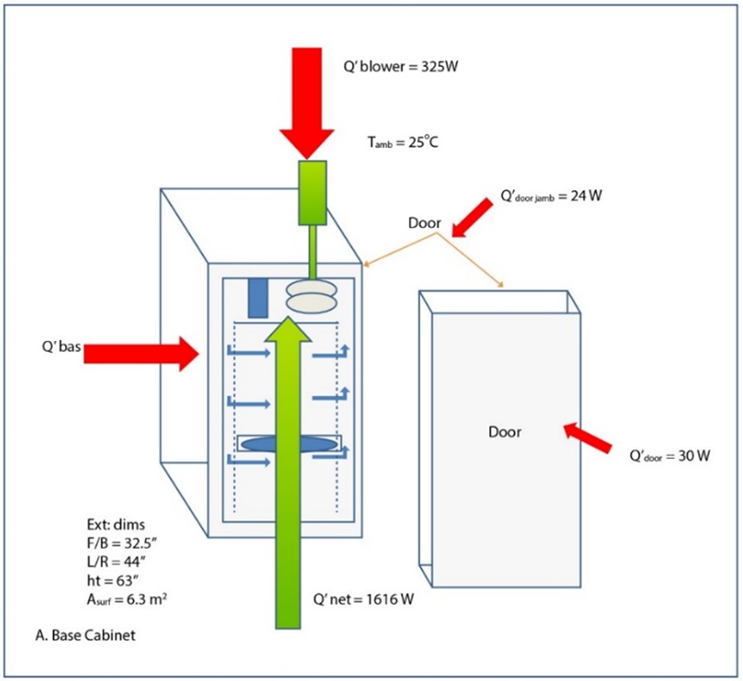
Figure 1: Rate chamber schematic
The refrigeration system in this example is designed to handle a total heat load of 2,100 W at minus 80°C. With a cabinet heat load of 158 W (similar to a conventional ULT) and an added blower heat load of 325 W, the total steady state heat load of the freezer measures 483 W. This leaves 1,617 W as this freezer’s capacity or buffer for loading of warm DS and/or door openings, an increase of over 1,800% over the 158 W of a conventional ULT freezer.
The second calculation required to assess freezer performance is how much heat removal is required to freeze bulk DS. For this analysis, a 10-L carboy filled with 8 L of water will be used as a typical example. Freezing 8 L of water from 25°C to minus 80°C requires the removal of 4.7 million Joules of energy (Q = m x Cp x ΔT). The heat removal rate is more difficult to calculate. One approach is to look at an ideal case of the freezer being able to remove heat at its full capacity, which is calculated above as 85 W for a typical ULT and 1,617 W for the blast freezer example. This calculation yields 15 hours to freeze the 8-L carboy for the ULT and 0.8 hours for the blast freezer. This is an ideal case and actual freeze times will be longer, but it highlights the differences in freezing potential between freezer types.
A second more rigorous approach is to calculate the heat transfer rate between the 8-L carboy and the freezer. There are three heat transfer resistances in the freezing process – convective heat transfer from the liquid to the inside container wall, conduction through the wall, and convection from the outside wall to the cold air. If we focus on the freezing process when freezing first starts (liquid at 0°C and freezer air at minus 80°C) the primary heat transfer resistance is from the container wall to the chamber air. This can be calculated from the following equation:
Q = U x A x ΔT
Where:
U is the convective heat transfer coefficient.
A is the area of the filled container wall exposed to chamber air.
ΔT is the difference in temperature.
The heat transfer coefficient for free convection (the stagnant air in a ULT chamber) is ~10 W/m^2/C. The heat transfer coefficient for forced convection, like that found in a blast freezer, can be two to five times higher than for free convection. To be conservative, a coefficient of 20 W/m^2/C will be used in the calculations.
The results of this second approach show the possible heat transfer rate from a 10L carboy is 100 W in free convection and 200 W with forced air convection. If this is compared to the heat removal capacity of the freezers, the ULT’s capacity of 85 W is only 85% of that required to remove the heat as quickly as possible. For the blast freezer example, the capacity of 1,617 W is eight times that required, or sufficient to remove the heat from eight carboys (at twice the rate). And in addition to freezing at twice the rate, the forced air in a blast freezer provides more uniform cooling throughout the chamber, providing more uniform freezing between DS containers.
In addition to the significantly longer and variable freezing times in a conventional ULT freezer, there are additional mechanical reliability concerns when using a conventional ULT freezer for freezing bulk DS. The long freezing times result in the compressor running constantly for many days during times of high energy expenditure, which can lead to overheating and premature failure of the refrigeration system. The failure mode is known as oil logging of the refrigeration system, leading to lack of cold refrigerant to cool down the compressor and compressor failure.
Figure 2 summarizes the differences between standard ULT freezers and freezers with forced air. convection.
Figure 2: Differences between forced air convection freezers and standard ULT freezers
Part 2: Contemporary Strategies For Storing Already-Frozen Drug Substance
After the DS freezing process, the frozen containers must be stored at minus 70°C to minus 80°C until the DS is required to be filled into drug product. This can typically be on the order of six months in storage. Until recently, there were two traditional approaches to holding frozen DS. The first was in conventional ULT freezers, which have the advantage of low capital cost and short delivery times but the disadvantage of requiring many freezers because of small storage capacity, leading to larger facility footprints, high qualification and validation costs, and many temperature points to calibrate and monitor. The second traditional approach is in large custom-designed freezers, which address the shortcomings of the ULT freezer approach but at the disadvantage of much higher capital cost and longer delivery times.
Recently, new technology bridged the gap between capacity-strained ULT freezers and unlimited-capacity custom installations. Sometimes called ultra-low chamber (ULC) freezers, these designs have around seven times the storage capacity of a standard ~27 cu. ft. ULT, but they are smaller than typical custom-designed units. There are pros and cons to each approach and the correct solution for each end user can be difficult to determine. One approach to finding the optimum solution is an economic evaluation using a discounted cash flow (net present cost) approach. In this approach, the cost of each option over 20 years is determined, and then the net present cost is calculated at a discount rate (typically around 10%). The costs considered include the initial capital cost for the freezers and facility, the electrical operating cost, the cost for initial IQ/OQ/validation, monitoring costs, and maintenance costs. The result of this calculation is shown in Figure 3 below:
Figure 3: Economic evaluation of DS frozen storage options
Figure 3 shows the correct frozen storage solution varies depending on the amount of freezer capacity required. For small applications where fewer than five ULT freezers are required, conventional ULT freezers have the lowest overall cost. For very large applications where more than 100 ULT freezers would be required, large custom freezers start to show a cost advantage.
And in the middle, between five and 100 freezers, the ULC solution is optimal. The above is based on an example case of assumptions and costs, and results will vary based on each end user’s actual costs; however, it is a typical case and shows the power of using economic evaluations.
Conclusion
Conventional ULT freezers are used for freezing and storage of biopharmaceutical bulk DS, but they are not always the optimal solution. ULT freezers are designed for storing frozen material and have limited capacity for freezing liquid DS.
For freezing bulk DS, forced air convection freezers that are designed for the application provide much faster freezing rates, much more consistent freezing rates, and greater mechanical reliability.
For storage of bulk DS, there are now three options available – conventional ULT freezers, large custom freezers, and a newer option of midsize ULC freezers. There are pros and cons to each option, and one tool to find the optimal solution is an economic evaluation. The results of an example evaluation show the optimum solution varies with the amount of freezer capacity required. For a small freezer capacity requirement (around five ULT freezers or fewer), ULT freezers provide the lowest overall cost. For very large applications where more than 100 ULT freezers would be required, the large custom freezers are optimal. And when freezer capacity of between five and 100 ULT freezers is required, the ULC freezer option gives the lowest overall cost.
About the Author:
Jeff Johnson is president of Biotech Design LLC, a bioprocess engineering consultancy. Previously he was with Merck & Co. Inc, where he was new technology lead and director, Global Engineering Solutions, responsible for the assessment of new manufacturing technology for Merck's vaccine, biologics, and sterile manufacturing processes. He co-led SUN-Merck's Single Use Technology Initiative, and the Process Technology Innovation Community of Practice. Prior roles at Merck include director of bioprocess engineering, responsible for business case and concept development for new vaccine and biologics capital projects, director of network management for therapeutic protein commercialization, and the technology transfer team leader for Gardasil. Prior to Merck, he worked for Genzyme Corp., Raytheon Engineers, Koch Engineering, and ARCO Chemical Co. He holds a BS in chemical engineering from the University of Rochester, an MS in chemical engineering from the University of Pennsylvania, and a certificate in biotechnology from Tufts University.