Identifying Outliers In Process Data Using Visual And Analytical Techniques
By Mark Durivage, Quality Systems Compliance LLC
Identifying outlier data points using visual and analytical techniques is especially important for proper process validation,  control, and monitoring in the FDA regulated industries. Additionally, properly identifying outliers can assist FDA regulated companies with the proper establishment of trending and excursion limits for complaint and nonconformance management, and other aspects such as environmental monitoring, which can trigger investigations or initiate the formal corrective and preventive action (CAPA) process.
control, and monitoring in the FDA regulated industries. Additionally, properly identifying outliers can assist FDA regulated companies with the proper establishment of trending and excursion limits for complaint and nonconformance management, and other aspects such as environmental monitoring, which can trigger investigations or initiate the formal corrective and preventive action (CAPA) process.
Outliers are data points that do not appear to “belong” to a given set of data. Outliers can be caused by recording and measurement errors, incorrect distribution assumption, unknown data structure, or novel phenomenon (Iglewicz, 1993). Additionally, outliers can be created by a shift in the mean or a change in the variation. There are several tools used to identify and detect outliers, including visual and analytical methods. Visual methods include histogram and box plots. Analytical methods include parametric and nonparametric techniques. Visual and analytical techniques can help to determine whether a suspect point is truly an outlier and should be removed from consideration when analyzing a data set.
Once an observation is identified (by means of a graphical or visual inspection) as a potential outlier, root cause analysis should begin to determine whether an assignable cause can be found for the spurious result (Walfish, 2006). This article will present some techniques for identifying outlier data points using visual, parametric, and nonparametric analytical techniques.
It should be noted that a confirmed outlier data point should never be deleted; however, it should be excluded from any subsequent calculations. Best practice is to provide the rationale and the method used to determine if the suspect point(s) is/are indeed outliers and document the cause(s) for the outlier(s).
Outliers Overview
Occasionally, a process will drift or even go out of control, indicating the presence of special cause variation. When the process does go out of control, the data points may be considered outliers. Outliers should be investigated and removed from the data set used to make the calculations for the process centerline, the control limits, or trend limits. Using the outlier data (special cause variation) can affect the centerline, control limits, and trend limit values. Excluding outlier data points will help with the elimination of bonus statistical tolerance.
We need to identify and consider excluding outlier data points:
- to provide a realistic picture of a process
- to provide meaningful control limits
- to prevent “bonus” statistical control limits
- to ensure actions are taken only when appropriate
There are several visual and analytical tools that can be used to determine whether the suspect points are indeed outliers. Each outlier detection method has certain rules and unique applications.
Visual Outlier Detection Methods
Visual outlier detection methods include normal curves, control charts, and box plots. An example of each visual method is provided.
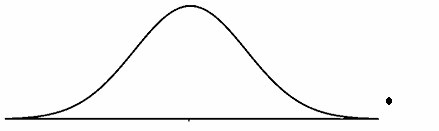
Figure 1: Normal curve with an outlier
The normal curve shown in Figure 1 has an outlier to the far right of the normal curve. Please note the point is above the axis to provide clarity.
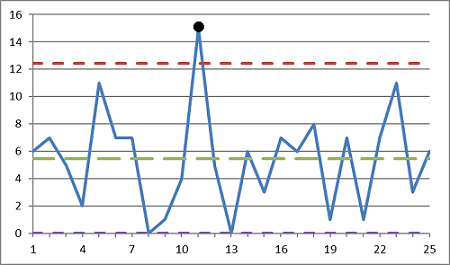
Figure 2: Control chart with an outlier
The control chart shown in Figure 2 has an outlier at Point 11.
Figure 3: Box plot with an outlier
The box plot shown in Figure 3 has an outlier at value 76.5.
Parametric Outlier Detection Methods
There are several parametric outlier detection methods, including:
- Outlier detection based on the standard deviation for a normal distribution
- Discordance outlier test
- Dean and Dixon outlier test
- Grubbs outlier test
Outlier Detection Based On The Standard Deviation For A Normal Distribution
One of the easiest methods for detecting an outlier is to use the standard deviation method. If the data is normally distributed, a single value may be considered an outlier if it falls outside of ± 3σ (approximately 99.8 percent of normally distributed data fall within this range).
Discordance Outlier Test
The discordance test for outliers is similar to the standard deviation method with the exception that a D statistic is calculated and compared to a table value using a stated level of confidence (usually 90 or 95 percent). This test assumes a normal distribution.
Dean And Dixon Outlier Test
The Dean and Dixon outlier test is a valid method for detecting outliers when the data is normally distributed. To use this test, the data must be ordered from smallest value to largest value. There are four different formulas used for this method. The formulas are dependent on the sample size. The calculated value is compared to a table value with a stated level of confidence.
Grubbs Outlier Test
The Grubbs outlier test computes the outlying data point using the average and standard deviation and then compares the calculated value against a critical table value. When a data point is deemed an outlier and removed from the data set, and an additional outlier is suspected, the average and standard deviation must be recalculated. The calculated value is compared to a table value with a stated level of confidence.
Nonparametric Outlier Detection Methods
There are several nonparametric outlier detection methods, including:
- Outlier detection based on the standard deviation for an unknown distribution
- Outlier detection based on the interquartile range
- Dixon’s Q test
- Walsh’s outlier test
- Hampel’s method for outlier detection
Outlier Detection Based On The Standard Deviation For An Unknown Distribution
Chebyshev’s inequality theorem can be used to determine if a point is an outlier when the underlying distribution is unknown. This method can also be used with a normal distribution; however, this method is not as sensitive as the standard deviation method. Chebyshev’s theorem states that the portion of any set of data within k standard deviations of the mean is always at least 1 – (1/k2), when k is > 1.
Outlier Detection Based On The Interquartile Range
Another method for detecting an outlier when the underlying distribution is unknown and assumed to be non-normal is the interquartile range method. If a suspected point is at least 1.5 interquartile ranges below the first quartile (Q1) or at least 1.5 interquartile ranges above the third quartile (Q3), the point may be considered an outlier.
Dixon’s Q Test
Dixon’s Q test is a method that compares the gap (data point in question to the next closest value) divided by the range to determine if the suspect point is an outlier. It is recommended to use this method only once on a particular set of data. Once the Q value has been calculated, it must be compared to the critical table value. If Q calculated > Q critical, the data point may be considered an outlier with the chosen confidence.
Walsh’s Outlier Test
Walsh’s outlier test is a nonparametric test that can be used to detect multiple outliers when the data is not normally distributed. This test requires a minimum sample size of 60. When the sample size (n) is between 60 and 219, the α level of significance is 0.10. When the sample size (n) is 220 or larger, the α level of significance is 0.05. To begin the process, the data must be ordered from smallest to largest. This test requires several calculations and is somewhat cumbersome.
Hampel’s Method For Outlier Detection
Because the mean and standard deviation are adversely influenced by the presence of outliers, Hampel’s method is presented (Hampel 1971; Hampel 1974). For example, the mean will be offset toward the outlier and the standard deviation will be inflated, leading to errant statistical decisions. Hampel’s method is somewhat resistant to these issues as the calculations use the median and median absolute deviation (MAD) to detect the presence of outliers.
To determine which, if any, values are outliers, calculate the median value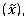 calculate the MAD =
calculate the MAD = 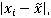 and finally calculate the decision value (median MAD * 5.2). Compare the calculated MAD values to the decision value. Any MAD that exceeds the decision value can be considered an outlier.
and finally calculate the decision value (median MAD * 5.2). Compare the calculated MAD values to the decision value. Any MAD that exceeds the decision value can be considered an outlier.
Conclusion
The discussion above focuses on identifying outlier data points. Visual and analytical techniques can help to determine whether a suspect point is truly an outlier and should be removed from consideration when analyzing a data set to help:
- provide a realistic picture of a process
- provide meaningful control limits
- prevent bonus statistical control limits
- ensure actions are taken only when appropriate
For small sets of data, manual calculations can suffice. However, when data sets are very large, the use of spreadsheets or statistical software applications should be considered.
I cannot emphasize enough the importance of documenting the tools and methods used. The visual and analytical tools presented in this article can and should be utilized based upon industry practice, guidance documents, and regulatory requirements.
About The Author:
 Mark Allen Durivage is the managing principal consultant at Quality Systems Compliance LLC and an author of several quality-related books. He earned a BAS in computer aided machining from Siena Heights University and an MS in quality management from Eastern Michigan University. Durivage is an ASQ Fellow and holds several ASQ certifications, including CQM/OE, CRE, CQE, CQA, CHA, CBA, CPGP, CSQP, and CSSBB. He also is a Certified Tissue Bank Specialist (CTBS) and holds a Global Regulatory Affairs Certification (RAC). Durivage resides in Lambertville, Michigan. Please feel free to email him at mark.durivage@qscompliance.com with any questions or comments, or connect with him on LinkedIn.
Mark Allen Durivage is the managing principal consultant at Quality Systems Compliance LLC and an author of several quality-related books. He earned a BAS in computer aided machining from Siena Heights University and an MS in quality management from Eastern Michigan University. Durivage is an ASQ Fellow and holds several ASQ certifications, including CQM/OE, CRE, CQE, CQA, CHA, CBA, CPGP, CSQP, and CSSBB. He also is a Certified Tissue Bank Specialist (CTBS) and holds a Global Regulatory Affairs Certification (RAC). Durivage resides in Lambertville, Michigan. Please feel free to email him at mark.durivage@qscompliance.com with any questions or comments, or connect with him on LinkedIn.
References:
- Durivage, M.A., 2014, Practical Engineering, Process, and Reliability Statistics, Milwaukee, ASQ Quality Press
- Durivage, M.A., 2017, Using Trending As A Tool For Risk-Based Thinking, Life Science Connect
- Hampel, Frank R. 1971. “A General Qualitative Definition of Robustness.” Annals of Mathematical Statistics 42 (6): 1887–96.
- Hampel, Frank R. 1974. “The Influence Curve and Its Role in Robust Estimation.” Journal of the American Statistical Association 69 (346): 383–93.
- Statistical Association 69 (346): 383–93.
- Iglewicz, Boris, and David Caster Hoaglin, 1993, How to Detect and Handle Outliers. Milwaukee: ASQ Quality Press.
- Walfish, Steven. 2006. “A Review of Statistical Outlier Methods.” Pharmaceutical Technology (November).
